La criptografía moderna es una rama de la criptografía que se centra en el estudio y diseño de algoritmos criptográficos seguros y eficientes para proteger la información en la era digital. Se basa en la teoría matemática y en los avances tecnológicos para garantizar la confidencialidad, integridad y autenticidad de los datos en transmisión y almacenamiento.
Entre los principales objetivos de la criptografía moderna se encuentran:
- Proporcionar privacidad y seguridad en la comunicación electrónica.
- Proteger la información sensible en redes y sistemas informáticos.
- Garantizar la autenticidad y la integridad de los datos.
- Permitir el acceso controlado a los recursos protegidos por sistemas de seguridad.
- Diseñar algoritmos y protocolos criptográficos robustos y eficientes.
- Investigar nuevas técnicas criptográficas que puedan superar las limitaciones actuales.
Algoritmo de intercambio de clave
En este ejemplo se explica un algoritmo que permite a Alice y Bob acordar una clave privada a partir de únicamente comunicaciones públicas. Partiendo de una clave pública común que es visible para todo el mundo y una clave privada para cada uno de ellos, Alice y Bob pueden llegar a obtener una clave privada común que sea imposible de descifrar para Eve, incluso aunque ella haya escuchado todas las interacciones entre ellos y conozca la clave pública.
Este ejemplo está inspirado en la propuesta de Diffie y Hellman en 1976, y se basa en una alegoría con pinturas de colores.
- Alice y Bob acuerdan de manera pública una pintura de color azul marino. Esta será la clave pública y es visible por todo el mundo, incluida Eve.
En este primer paso, Alice y Bob establecen una clave pública que será visible para todos. En el ejemplo se utiliza una pintura de color azul marino, pero en la criptografía real se utiliza una clave pública que puede ser un número, una palabra, una secuencia de caracteres, etc.
- Tanto Alice como Bob tienen cada uno una clave privada que solo ellos conocen. En el caso de Alice su clave es una pintura de color naranja.
En este segundo paso, Alice y Bob generan cada uno su propia clave privada, que es secreta y solo conocida por ellos. En el ejemplo, Alice tiene una clave privada que es una pintura de color naranja, pero en la criptografía real la clave privada es un valor secreto generado de forma aleatoria.
- Alice puede mezclar su pintura naranja con la pintura azul en iguales cantidades y obtener una nueva pintura de color morado. Lo importante aquí es que este proceso de mezclar no es reversible, aunque se conozca el color final (morado) y uno de los iniciales (azul) es muy complicado deducir el otro color inicial (naranja).
En este tercer paso, Alice mezcla su clave privada con la clave pública (la pintura azul) para generar una nueva clave que es una mezcla de ambas. En el ejemplo, la clave resultante es una pintura de color morado, que es el resultado de mezclar en partes iguales la pintura naranja y la pintura azul. Es fundamental destacar que este proceso de mezcla es irreversible, lo que significa que es muy difícil deducir la clave privada original a partir de la clave resultante.
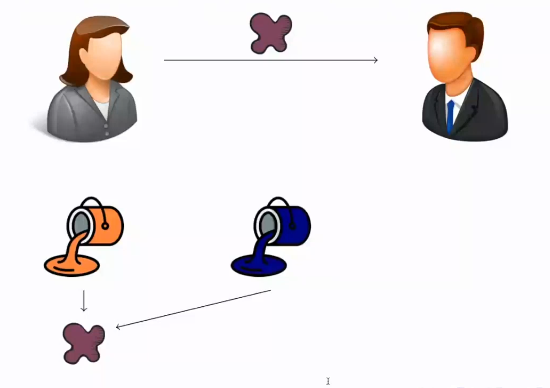
- Alice envía esta mezcla de la clave pública y su privada a Bob.
Alice envía la mezcla que ha obtenido a Bob. Este valor enviado no es secreto, ya que se trata de una combinación de la clave pública y su clave privada, que sólo ella conoce.
- Bob hace lo mismo que Alice. Su pintura privada es de color verde claro, que mezclado con el azul marino público da lugar a un verde oscuro que manda a Alice.
Bob mezcla su clave privada con la clave pública, obteniendo un nuevo valor. En este ejemplo, la clave privada de Bob es una pintura de color verde claro, que mezclada con la clave pública da lugar a un nuevo valor de color verde oscuro. Bob envía este nuevo valor a Alice.
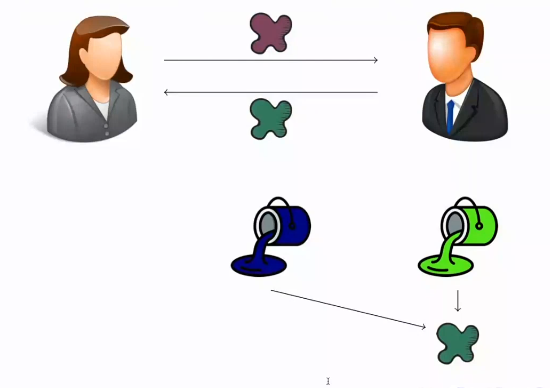
- Alice, tras recibir la mezcla de Bob, la mezcla con su propia pintura de manera que los tres colores tengan la misma proporción, obteniendo un marrón verdoso.
Alice mezcla el valor enviado por Bob con su propio valor, obteniendo un nuevo valor que es una combinación de los tres colores: naranja, azul y verde oscuro. En este ejemplo, Alice mezcla los tres valores de manera que tienen la misma proporción, obteniendo un nuevo valor de color marrón verdoso.
- Bob hace lo mismo con la mezcla de Alice y obtiene el mismo color de ella, ya que el marrón verdoso es una mezcla de los tres colores en la misma proporción.
En este punto, Alice y Bob han obtenido un color común (marrón verdoso) a partir de intercambiar sus claves privadas utilizando la clave pública y sin necesidad de ningún otro canal seguro. Este color común es en realidad una clave secreta compartida que Alice y Bob pueden utilizar para comunicarse de manera segura, por ejemplo, utilizando un sistema de cifrado simétrico en el que ambas partes cifran y descifran los mensajes utilizando la misma clave.
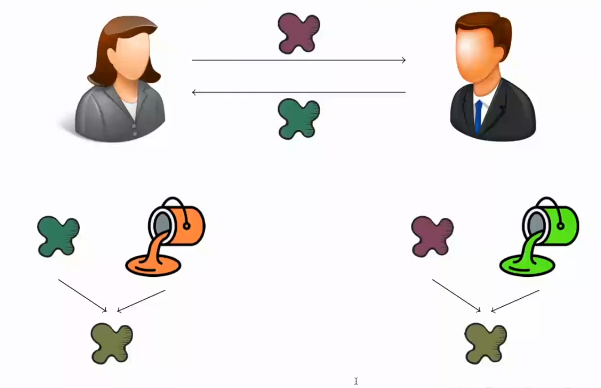
Al terminar, Alice y Bob han conseguido llegar a un mismo color a partir de hacer intercambio público de pintura, y aunque Eve haya interceptado todas las pinturas que ambos se han enviado, nunca podría obtener el color final, ya que no conoce ninguno de los colores privados. El algoritmo de intercambio de clave de Diffie-Hellman es utilizado en muchos protocolos criptográficos modernos para establecer claves de sesión seguras que son utilizadas en sistemas de cifrado simétricos. El algoritmo se basa en la dificultad de calcular la clave privada a partir de la clave pública, lo que lo hace seguro incluso si Eve es capaz de interceptar todas las comunicaciones públicas entre Alice y Bob.
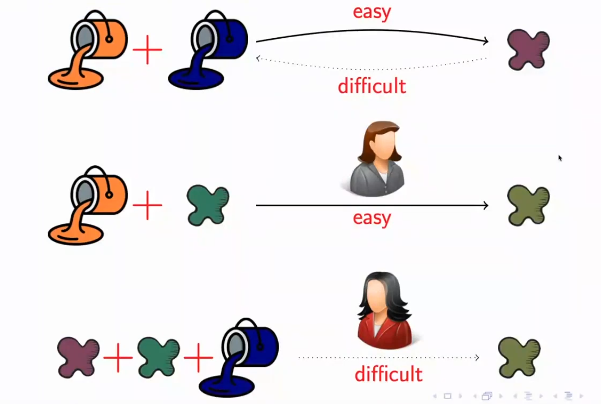
En el ejemplo de la pintura y las claves criptográficas se utiliza una operación que es fácil de realizar (mezclar dos colores) pero difícil de deshacer sin conocer los colores originales utilizados. Esta misma idea puede ser aplicada a sistemas matemáticos reales, donde se utilizan operaciones matemáticas que son fáciles de realizar pero muy difíciles de deshacer sin conocer información privada. Por ejemplo, en la criptografía moderna se utilizan algoritmos como RSA, que se basan en la dificultad de factorizar números grandes en números primos. La operación de multiplicar dos números primos es fácil de realizar, pero encontrar los dos factores primos de un número muy grande es una tarea computacionalmente muy costosa. Por lo tanto, el algoritmo RSA es seguro mientras sea difícil factorizar números grandes en tiempo razonable.
En general, en la criptografía moderna se utilizan operaciones matemáticas como exponenciación modular, funciones hash criptográficas, curvas elípticas, entre otras, que son fáciles de realizar pero muy difíciles de invertir sin conocer cierta información privada.
Grupos computacionales
En el contexto de la criptografía, los grupos son empleados para generar claves públicas y privadas mediante algoritmos de cifrado. El grupo se utiliza como un espacio de trabajo para los cálculos necesarios para la generación de claves. Un ejemplo de grupo utilizado en criptografía es el grupo multiplicativo de los números enteros módulo, un número primo p. Este grupo se denota como Zp* y se define como el conjunto de enteros positivos menores que «p» que son coprimos con «p». La operación en este grupo es la multiplicación módulo «p».
En la criptografía de clave pública, se utiliza la dificultad del problema de la factorización de enteros grandes para generar claves. El algoritmo RSA, por ejemplo, utiliza dos números primos grandes para generar una clave pública y una clave privada. Estos dos números primos se utilizan para construir el grupo Zn* donde n es el producto de los dos números primos. La clave pública es un número en Zn* y la clave privada es un número que solamente el propietario de la clave puede calcular.
Los grupos también se utilizan en otros algoritmos de cifrado, como el Diffie-Hellman, que utiliza un grupo multiplicativo de enteros módulo, un número primo para generar claves compartidas entre dos partes. En este algoritmo, ambas partes acuerdan un número primo y un elemento del grupo y utilizan operaciones matemáticas en el grupo para generar una clave compartida.
En informática y criptografía, se utilizan grupos finitos y cíclicos para implementar diferentes protocolos de seguridad. Estos grupos tienen una estructura matemática específica que les permite cumplir con ciertas propiedades necesarias para la criptografía.
En un grupo cíclico, existe un elemento neutro (denotado como 1) y un elemento generador (denotado como g), que permite generar todos los demás elementos del grupo mediante operaciones de exponenciación. Es decir, la operación en este grupo consiste en elevar el generador a un número entero positivo o negativo. Si el grupo tiene un total de p elementos, entonces el generador g debe cumplir con la propiedad de que g^p = 1, donde 1 representa el elemento neutro del grupo.
Esta propiedad asegura que los elementos generados por el grupo cíclico son finitos y que, después de elevar el generador a una potencia p, el resultado vuelve a ser el elemento neutro. Además, el hecho de que el grupo sea cíclico significa que cualquier elemento del grupo se puede expresar como una potencia del generador g elevado a un número entero.
En criptografía, estos grupos finitos y cíclicos se utilizan para construir sistemas criptográficos como el intercambio de claves de Diffie-Hellman y la firma digital ElGamal. Estos protocolos de seguridad aprovechan las propiedades matemáticas de los grupos cíclicos para realizar operaciones de manera segura y proteger la información transmitida.
Podemos replicar el proceso anterior de la pintura usando estos elementos matemáticos.
En este caso, Alice y Bob acuerdan públicamente una base o generador g y un número primo p. Estos elementos conforman el grupo finito y cíclico empleado para realizar el intercambio de claves.
Cada uno de ellos tiene un exponente privado, a y b respectivamente, que son elegidos de forma aleatoria. Luego, Alice calcula g elevado a la potencia de su exponente privado (g^a) y envía este valor a Bob a través de un canal público. De manera similar, Bob calcula g elevado a la potencia de su exponente privado (g^b) y envía este valor a Alice. Una vez que ambos tienen estos valores, Alice calcula (g^b)^a y Bob calcula (g^a)^b, lo que resulta en el mismo valor común secreto para ambos: g^(ab). Este valor común secreto puede ser utilizado como una clave para encriptar y desencriptar mensajes de forma segura.
En resumen, empleando grupos finitos y cíclicos, podemos replicar el proceso de intercambio de claves de Diffie-Hellman de forma matemática y segura. Los exponentes privados de cada parte son la clave secreta que permite llegar a un valor común secreto sin que Eve pueda interceptarla o deducirla.
