In federated learning, a central server organizes the training process and receives contributions from all clients, thus potentially also representing a single point of failure. Thus, a reliable and powerful central server may not always be available or desirable in more collaborative learning scenarios, and may even become a bottleneck when the number of clients is very large.
The key idea of fully decentralized learning is to replace communication with the server by peer-to-peer communication between individual clients.
In fully decentralized algorithms, a “round” corresponds to each client performing a local update and exchanging information with its neighbors in the graph. In the context of machine learning, the local update is usually a local (stochastic) gradient step and the communication consists of averaging the parameters of the local model with the neighbors.
Note that there is no longer a global state of the model as in standard federated learning, but the process can be designed so that all local models converge to the desired global solution, i.e. the individual models gradually reach consensus.
In the decentralized environment, a central authority may still be in charge of setting up the learning task to decide issues such as the model to train, the algorithm to use, the hyperparameters…. Alternatively, decisions can also be made by the client proposing the learning task, or collaboratively through a consensus scheme.
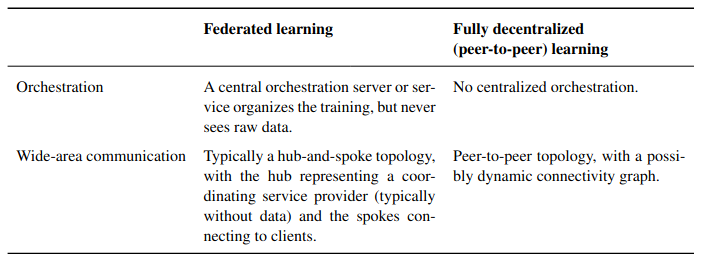 This table shows a comparison of the key distinctions between federated learning and fully decentralized learning.
This table shows a comparison of the key distinctions between federated learning and fully decentralized learning.
Algorithmic Challenges
A large number of important algorithmic questions remain open on the topic of real-world usability of decentralized schemes for machine learning.
Effect of network topology and asynchrony in decentralized DMSs.
Fully decentralized algorithms for learning must be robust to limited client availability (with clients temporarily unavailable, disconnecting or joining during execution) and limited network reliability (with possible message drops) .
Well-connected or denser networks promote faster consensus and provide better theoretical convergence rates, which depend on the spectral gap of the network graph. However, when the data are IID, more sparse topologies do not necessarily impair convergence in practice.
Most optimization theory work does not explicitly consider how topology affects runtime, i.e., the wall-clock time required to complete each SGD iteration.
Denser networks tend to suffer from communication delays that increase with node degrees.
The proposed MATCHA is a decentralized SGD method based on coincident decomposition sampling, which reduces the communication delay per iteration for any node topology while maintaining the same error convergence rate. The key idea is to decompose the graph topology into matches consisting of separate communication links that can operate in parallel and carefully choose a subset of these matches at each iteration.
Decentralized locally updated DMS
Theoretical analysis of schemes that perform multiple local update steps before a communication “round” is significantly more challenging than those using a single SGD step.
In general, understanding convergence under non-IDD data distributions and how to design a model averaging policy that achieves the fastest convergence remains an open problem.
Personalization and trust mechanisms.
Designing algorithms for learning customized model collections is an important task for non-IDI data distributions.
New articles have presented algorithms that help to collaboratively learn a personalized model for each client by smoothing model parameters between clients that have similar tasks (similar data distributions).
Despite advances, the robustness of such schemes to malicious actors or contribution of untrusted data or labels remains a key challenge, as the use of incentives or mechanism design in combination with decentralized learning is an emerging and important goal, which may be more difficult to achieve in the environment without a trusted central server.
Gradient quantization and compression methods.
In potential applications, clients would often be limited in terms of available communication bandwidth and allowable power usage.
Translating and generalizing some of the existing compressed communication schemes from the centralized orchestrator-facilitated environment to the fully decentralized environment, without negatively affecting convergence, is still one of the active lines of research, with one of the main solutions proposed being to design decentralized optimization algorithms that naturally result in few updates.
Privacy
A major challenge remains to prevent any client from reconstructing another client’s private data from its shared updates, while maintaining a good level of usefulness for the learned models.
Differential privacy is the standard approach to mitigate such privacy risks. In decentralized federated learning, this can be achieved by having each client aggregate noise locally, but unfortunately, such local privacy approaches often come at a large cost in utility. In addition, distributed methods based on secure aggregation or secure mixing that are designed to improve the tradeoff between utility and privacy in the standard FL setting do not easily integrate with fully decentralized algorithms.
Another possible direction to achieve better tradeoffs between privacy and utility in fully decentralized algorithms is to rely on decentralization itself to extend differential privacy guarantees, e.g., by considering appropriate local differential privacy relaxations.
Federated Learning: Practical challenges
An orthogonal question for fully decentralized learning is how it can be realized in practice.
Blockchain is a distributed ledger shared among disparate users, which makes digital transactions, including cryptocurrency transactions, possible without a central authority. In particular, smart contracts allow the execution of arbitrary code on the blockchain.
In terms of federated learning, the use of the technology could enable the decentralization of the global server by using smart contract to aggregate models, where the participating clients running them could be different companies or cloud services.
However, blockchain data is publicly available by default, which could discourage users from participating in the decentralized federated learning protocol, as data protection is often the main motivating factor.
To address such concerns, it might be possible to modify existing privacy-preserving techniques to fit the decentralized federated learning scenario.
First, to prevent participating nodes from exploiting individually submitted model updates, existing secure aggregation protocols could be used by effectively handling participant dropout at the cost of protocol complexity [Article].
An alternative system would be to have each client make a cryptocurrency deposit on the blockchain and be penalized if they drop out during execution. Without the need to handle dropouts, the secure aggregation protocol could be significantly simplified.
Another way to achieve secure aggregation is to use a confidential smart contract as enabled by the Oasis Protocol running inside secure enclaves. With this, each client could simply send an encrypted local model update, knowing that the model will be decrypted and aggregated within the secure hardware via remote certification.
To prevent a client from attempting to reconstruct another client’s private data by exploiting the global model, client-level differential privacy has been proposed. Client-level differential
privacy is achieved by adding random Gaussian noise in the aggregated global model that is sufficient to hide the update of any individual client.
In the blockchain context, each client could locally aggregate a certain amount of Gaussian noise after the local gradient descent steps and send the model to the blockchain. The local noise scale should be calculated so that the aggregated noise in blockchain can achieve the same differential privacy at the client level.
Finally, the global aggregated model in blockchain could be encrypted and only the participating clients have the decryption key, which protects the model from the public.
