Modern cryptography and key exchanges

Modern cryptography is a branch of cryptography that focuses on the study and design of secure and efficient cryptographic algorithms to protect information in the digital age. It is based on mathematical theory and technological advances to ensure the confidentiality, integrity, and authenticity of data in transmission and storage.

Among the main objectives of modern cryptography are:

• Providing privacy and security in electronic communication.
• Protecting sensitive information in networks and computer systems.
• Ensuring the authenticity and integrity of data.
• Enabling controlled access to resources protected by security systems.
• Design robust and efficient cryptographic algorithms and protocols.
• Investigate new cryptographic techniques that can overcome current limitations.

Key exchange algorithm

This example explains an algorithm that allows Alice and Bob to agree on a private key from only public communications. Starting from a common public key that is visible to everyone and a private key for each of them, Alice and Bob can arrive at a common private key that is impossible for Eve to decrypt, even though she has listened to all the interactions between them and knows the public key.

This example is inspired by Diffie and Hellman’s 1976 proposal, and is based on an allegory with coloured paints.

1. Alice and Bob publicly agree on a navy blue paint. This will be the public key and is visible to everyone, including Eve.

In this first step, Alice and Bob establish a public key that will be visible to everyone. In the example, a navy blue paint is used, but in real cryptography a public key is used, which can be a number, a word, a sequence of characters, etc.

2. Alice and Bob each have a private key that only they know. In Alice’s case, her key is an orange paint.

In this second step, Alice and Bob each generate their own private key, which is secret and known only to them. In the example, Alice has a private key that is an orange paint, but in real cryptography the private key is a randomly generated secret value.

3. Alice can mix her orange paint with the blue paint in equal amounts and get a new purple paint. The important thing here is that this mixing process is not reversible, even if the final colour (purple) and one of the initial colours (blue) are known, it is very complicated to deduce the other initial colour (orange).

In this third step, Alice mixes her private key with the public key (the blue paint) to generate a new key that is a mixture of both. In the example, the resulting key is a purple paint, which is the result of mixing equal parts of the orange paint and the blue paint. It is essential to note that this mixing process is irreversible, which means that it is very difficult to deduce the original private key from the resulting key.

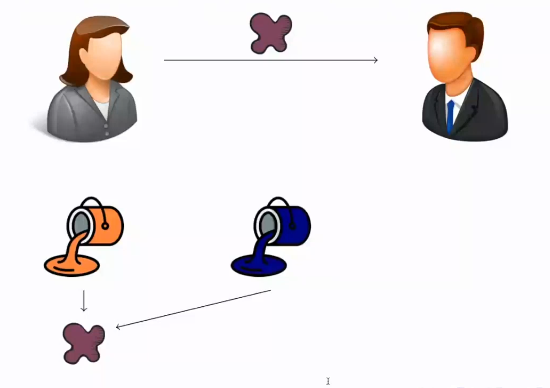
4. Alice sends this mix of the public key and her private key to Bob.

Alice sends the mix she has obtained to Bob. This value sent is not secret, as it is a combination of the public key and her private key, which only she knows.

5. Bob does the same as Alice. His private paint is light green, which, mixed with the public navy blue, results in a dark green, which he sends to Alice.

Bob mixes his private key with the public key, resulting in a new value. In this example, Bob’s private key is a light green paint, which mixed with the public key results in a new dark green value. Bob sends this new value to Alice.

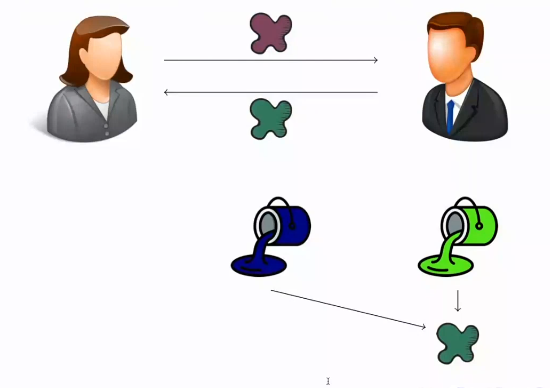
6. Alice, after receiving Bob’s mixture, mixes it with her own paint so that the three colours have the same proportion, resulting in a greenish brown.

Alice mixes the value sent by Bob with her own value, obtaining a new value that is a combination of the three colours: orange, blue and dark green. In this example, Alice mixes the three values so that they have the same ratio, resulting in a new greenish-brown value.

7. Bob does the same with Alice’s mixture and gets the same colour from her, since the greenish brown is a mixture of the three colours in the same proportion.

At this point, Alice and Bob have obtained a common colour (greenish brown) from exchanging their private keys using the public key and without the need for any other secure channel. This common colour is actually a shared secret key that Alice and Bob can use to communicate securely, for example, using a symmetric encryption system where both parties encrypt and decrypt messages using the same key.

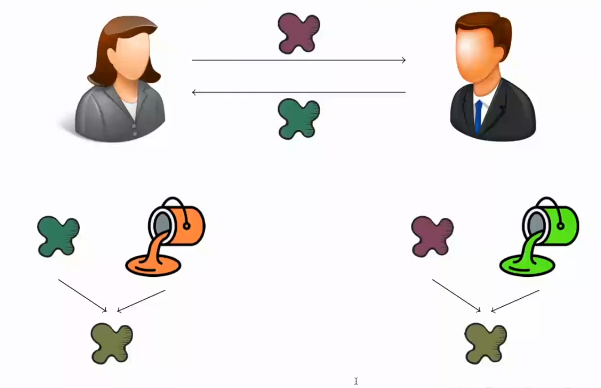
In the end, Alice and Bob have managed to arrive at the same colour by making a public exchange of paint, and even if Eve has intercepted all the paintings they have sent to each other, she could never get the final colour, as she does not know any of the private colours. The Diffie-Hellman key exchange algorithm is used in many modern cryptographic protocols to establish secure session keys that are used in symmetric encryption systems. The algorithm is based on the difficulty of calculating the private key from the public key, which makes it secure even if Eve is able to intercept all public communications between Alice and Bob.

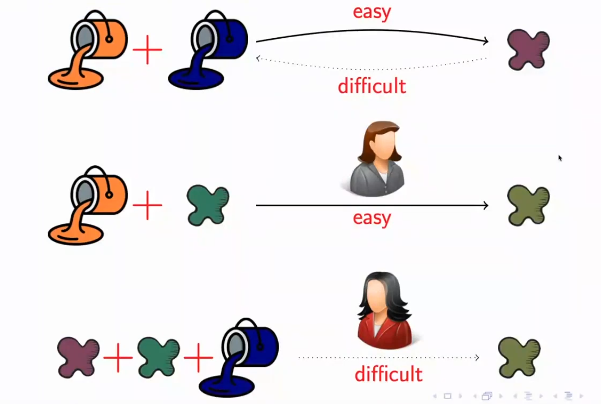
The example of painting and cryptographic keys uses an operation that is easy to perform (mixing two colours) but difficult to undo without knowing the original colours used. This same idea can be applied to real mathematical systems, where mathematical operations are used that are easy to perform but very difficult to undo without knowing private information. For example, modern cryptography uses algorithms such as RSA, which are based on the difficulty of factoring large numbers into prime numbers. The operation of multiplying two prime numbers is easy to perform, but finding the two prime factors of a very large number is a computationally very expensive task. Therefore, the RSA algorithm is secure as long as it is difficult to factor large numbers in reasonable time.

In general, modern cryptography uses mathematical operations such as modular exponentiation, cryptographic hash functions, elliptic curves, among others, which are easy to perform but very difficult to reverse without knowing some private information.

Computational groups

In the context of cryptography, groups are used to generate public and private keys by means of encryption algorithms. The group is used as a workspace for the computations necessary for key generation. An example of a group used in cryptography is the multiplicative group of integers modulo, a prime number p. This group is denoted as Zp* and is defined as the set of positive integers less than “p” that are coprime with “p”. The operation on this group is multiplication modulo “p”.

In public key cryptography, the difficulty of the large integer factorization problem is used to generate keys. The RSA algorithm, for example, uses two large prime numbers to generate a public key and a private key. These two prime numbers are used to construct the group Zn* where n is the product of the two prime numbers. The public key is a number in Zn* and the private key is a number that only the owner of the key can calculate.

Groups are also used in other encryption algorithms, such as Diffie-Hellman, which uses a multiplicative group of integers modulo a prime number to generate shared keys between two parties. In this algorithm, both parties agree on a prime number and an element of the group and use mathematical operations on the group to generate a shared key.

In computer science and cryptography, finite and cyclic groups are used to implement different security protocols. These groups have a specific mathematical structure that allows them to fulfil certain properties necessary for cryptography.

In a cyclic group, there is a neutral element (denoted as 1) and a generator element (denoted as g), which allows all the other elements of the group to be generated by exponentiation operations. That is, the operation in this group consists of raising the generator to a positive or negative integer. If the group has a total of p elements, then the generator g must satisfy the property that g^p = 1, where 1 represents the neutral element of the group.

This property ensures that the elements generated by the cyclic group are finite and that, after raising the generator to a power p, the result is again the neutral element. Furthermore, the fact that the group is cyclic means that any element of the group can be expressed as a power of the generator g raised to an integer.

In cryptography, these finite, cyclic groups are used to build cryptographic systems such as the Diffie-Hellman key exchange and the ElGamal digital signature. These security protocols take advantage of the mathematical properties of cyclic groups to securely perform operations and protect the transmitted information.

We can replicate the above painting process using these mathematical elements.

In this case, Alice and Bob publicly agree on a base or generator g and a prime number p. These elements form the finite, cyclic group used to perform the key exchange.

Each of them has a private exponent, a and b respectively, which are chosen at random. Alice then computes g to the power of her private exponent (g^a) and sends this value to Bob through a public channel. Similarly, Bob calculates g to the power of his private exponent (g^b) and sends this value to Alice. Once they both have these values, Alice calculates (g^b)^a and Bob calculates (g^a)^b, resulting in the same secret common value for both: g^(ab). This secret common value can be used as a key to securely encrypt and decrypt messages.

In summary, using finite and cyclic groups, we can replicate the Diffie-Hellman key exchange process mathematically and securely. The private exponents of each party are the secret key that allows us to arrive at a secret common value without Eve being able to intercept or deduce it.